The data structure behind terminals

Grids - two-dimensional arrays of characters - are the universal building blocks of terminals. The basic operations we expect from our terminals - entering a command, receiving output, scrolling through a file - are, at their core, operations on grids. This piece is an attempt at explaining the terminal from the bottom up, starting from the grid. The goal is to spell out some of the not-so-obvious performance calculus behind terminal grids: what are the operations being optimized and at what cost?

If a terminal session is really some conversation history between the terminal and the commands it has executed or is currently executing, then it’s the grid that provides some agreed-upon format or ledger to converse. It’s not just that grids are a convenient choice for terminal builders; the grid is actually what’s required by the program the terminal is layered over, the shell. The shell moves a cursor and outputs characters within a defined two-dimensional space, and the terminal is responsible for storing and rendering the contents of that space to the end-user. This makes the concept of the grid a – if not the – fundamental engineering specification of terminals.

(If you’re curious to learn more about the dependencies between terminals and shells, I recommend this blog post.)

In Warp, the grid is especially important because it’s everywhere. Warp separates commands into blocks, and each block consists of three grids: one for the prompt, one for the command input, and one for the command output. Even opening full-screen programs like vim and emacs are themselves instances of this same grid, just with expanded dimensions.

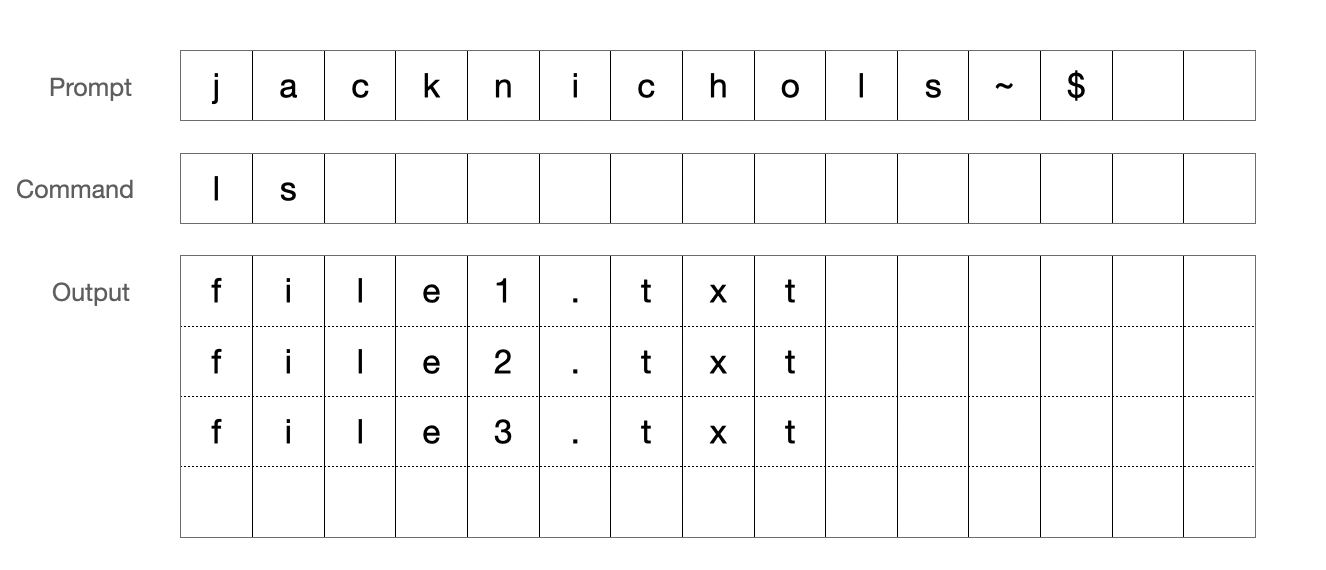
Here, a command in Warp is the combination of three grids receiving and sending characters to the shell. (Technical note: Warp also offers a default prompt instead of a customized shell prompt).

Because the grid is the means of storage and communication, it is at this layer that terminals make meaningful trade-offs around performance. For example, imagine you’re running a server that endlessly prints out log lines. When the log lines fill up the available grid space on the screen, how many new rows should Warp allocate for the grid? 1? 100? 1000? Allocating 1000 could buy us time before the command runs out of space again, saving us the performance penalty of repeated memory allocations, but of course the command might not use the full 1000. Should we risk a slightly greater memory footprint for an uncertain promise of faster execution? ¹

Even more interesting are the trade-offs the grid must make between the most basic terminal operations. Some examples of these operations are reading in data from the shell, scrolling through content, and resizing the screen or splitting panes. Warp’s implementation of the grid is itself an opinionated stance on which of these operations a terminal should be most efficient at, with the reality being that optimizing for one almost always means not optimizing for another. Should we be excellent at one thing if it means being just okay at something else? The grid is the layer at which this type of performance calculus is baked in and shipped to our users.

Getting technical²

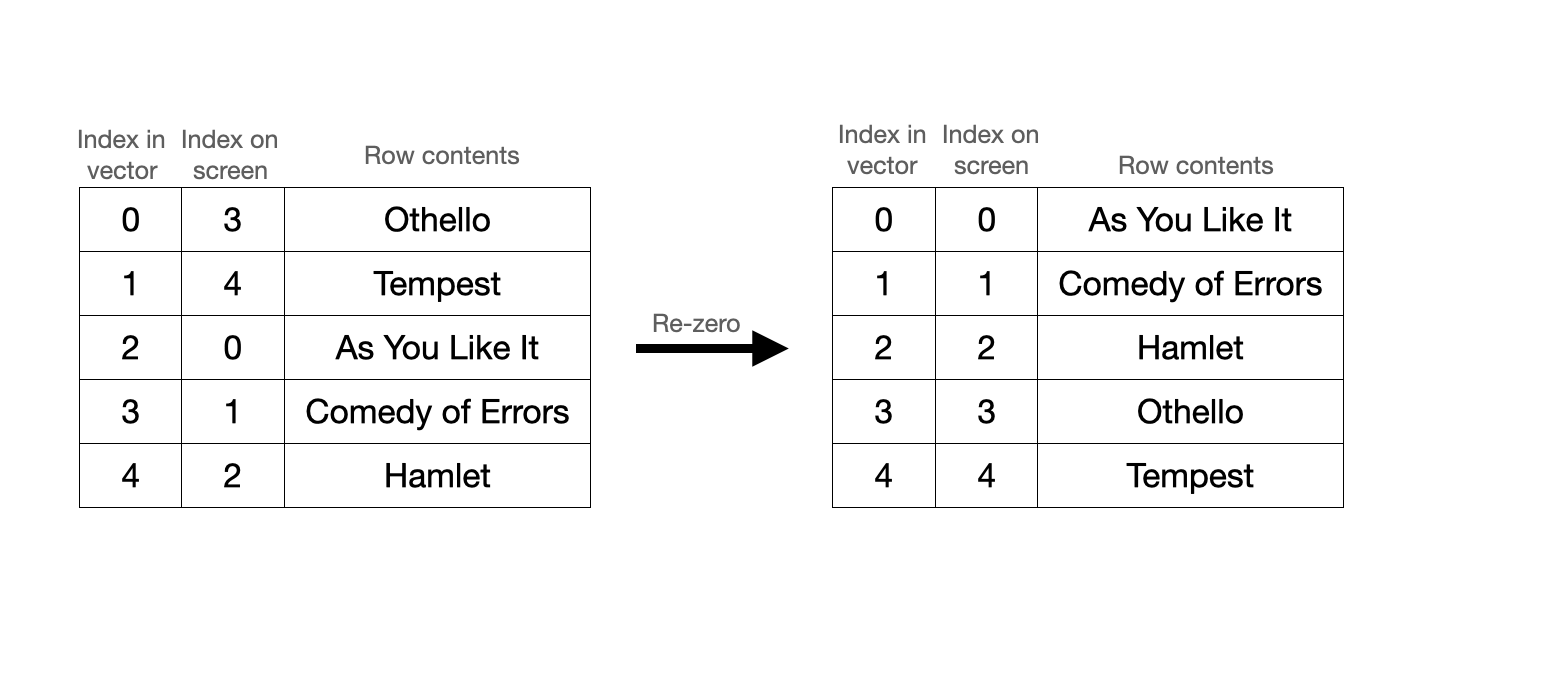
Warp’s grid is a circular buffer that stores rows sequentially ³ in a vector. Say, for example, you create a grid storing a subset of Shakespeare plays that are sorted alphabetically. How this renders on screen and how this is stored internally might look something like this:

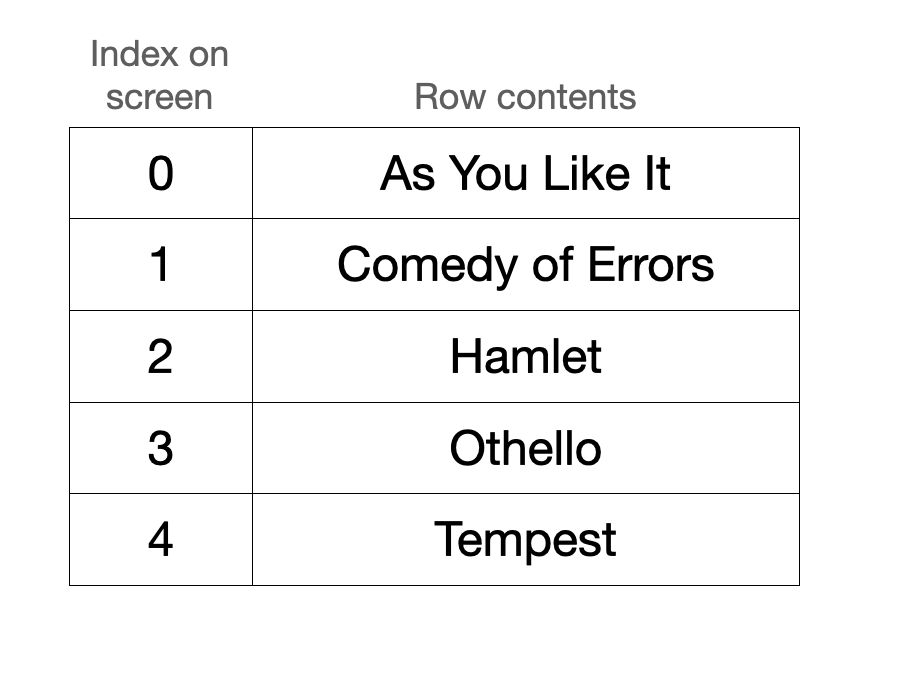
On screen, the contents are rendered alphabetically.

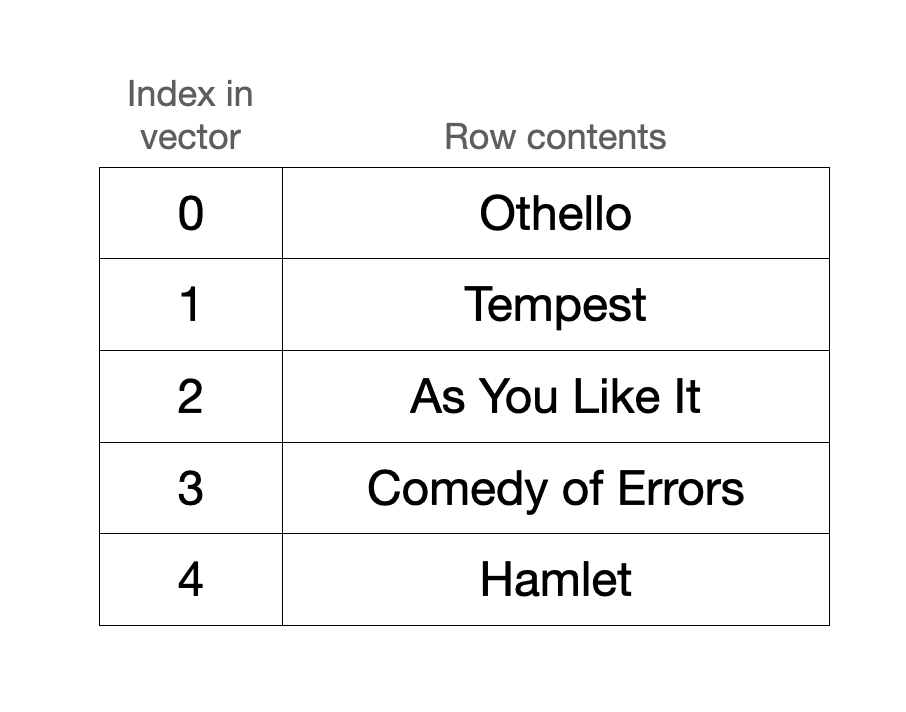
In storage (the underlying vector), the contents remain sequential but may be rotated. Notice the top row in the grid is stored at vector index 2, the second row is stored at vector index 3, and so on.

The conversion between the screen index and the vector index is a really, really important one. When the grid renders to the screen, we’ll want to locate the contents of screen index 0 and then 1 and then 2 and so on. To optimize for this, the grid stores two integers that allow us to efficiently translate between screen space and vector space.

bottom_row: the vector index of the last row in the grid, aka the furthest the grid extends. In the example, bottom_row = 1 (Tempest is the last row in the grid).
length: the total number of rows that we’ve received from the shell, which may be different from the actual capacity of the vector at any given moment. In the example, length = 5.

Using these indices, we can convert from screen space to vector space like this:

⁴

Nevertheless, the whole process of index conversions presupposes that the grid needs to be rotated in the first place. Why is that the case? Why not skip the silly conversions and enforce equivalence between the screen indices and the vector indices, meaning that “As You Like It,” the first row on screen, is also stored as the first row in the vector? Not surprisingly, this is because the grid is heavily optimizing for something else entirely: scrolling!

Scrolling the grid

In Warp, scrolling in a command like vim, emacs, git log, git diff, or many others ⁵ is optimized to avoid the ultimate price in the grid world – having to move physical memory. Inspired from the previous section, imagine an example of scrolling the contents of the Shakespeare file upwards to reveal a new row at the bottom of the screen:

‍

What would this look like at the grid layer? To start off, the underlying vector is unrotated. It looks like this, with bottom_row = 8 and the conceptual “top row” = 0.

The first step to scrolling up is to extend bottom_row by one while keeping length the same. When we wrap bottom_row, it becomes 0 and top row becomes 1.

From there, we overwrite the contents of the bottom row with whatever the shell feeds to Warp as the next line in the file – in this case, “Tempest”. After that, the scroll operation is finished and the resulting grid looks like this:

What’s noteworthy is that Warp completes this scroll operation without moving any data in the vector, besides overwriting the exiting row with the entering row. The scroll operation succeeded solely by changing the metadata of the grid, specifically the index of the bottom_row. The result is an extremely efficient scroll operation at the cost of leaving the grid in a rotated state.

One of the penalties of the now-rotated grid is the added complexity of index conversion that we discussed above. Broadly speaking, this penalty is relatively minor and is more than compensated for by the efficiency we gain during scrolling. Where this becomes a little bit more harrowing as a performance calculation is when we actually receive output from the shell and find ourselves needing an extra row. At that time, having a grid that’s rotated leaves us no choice but to move memory.

Extending the grid

A lot of terminal commands print content to the screen rapidly and require the size of the grid to grow dynamically.

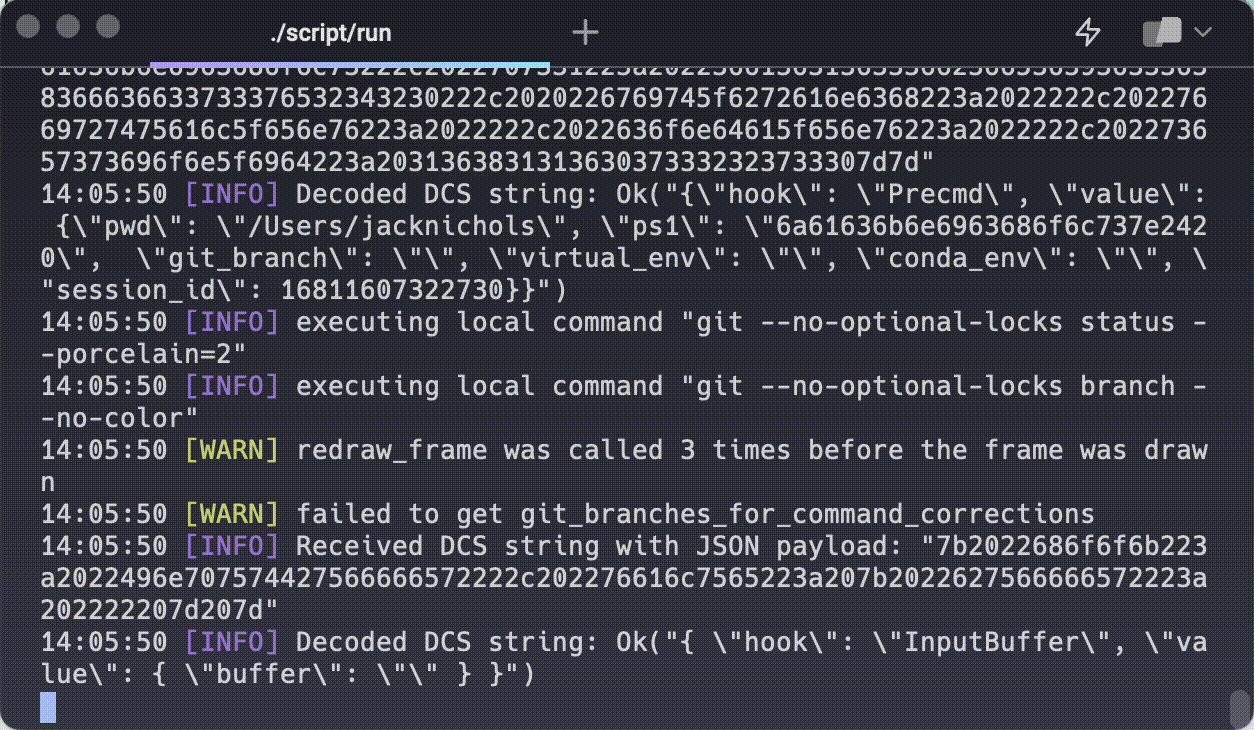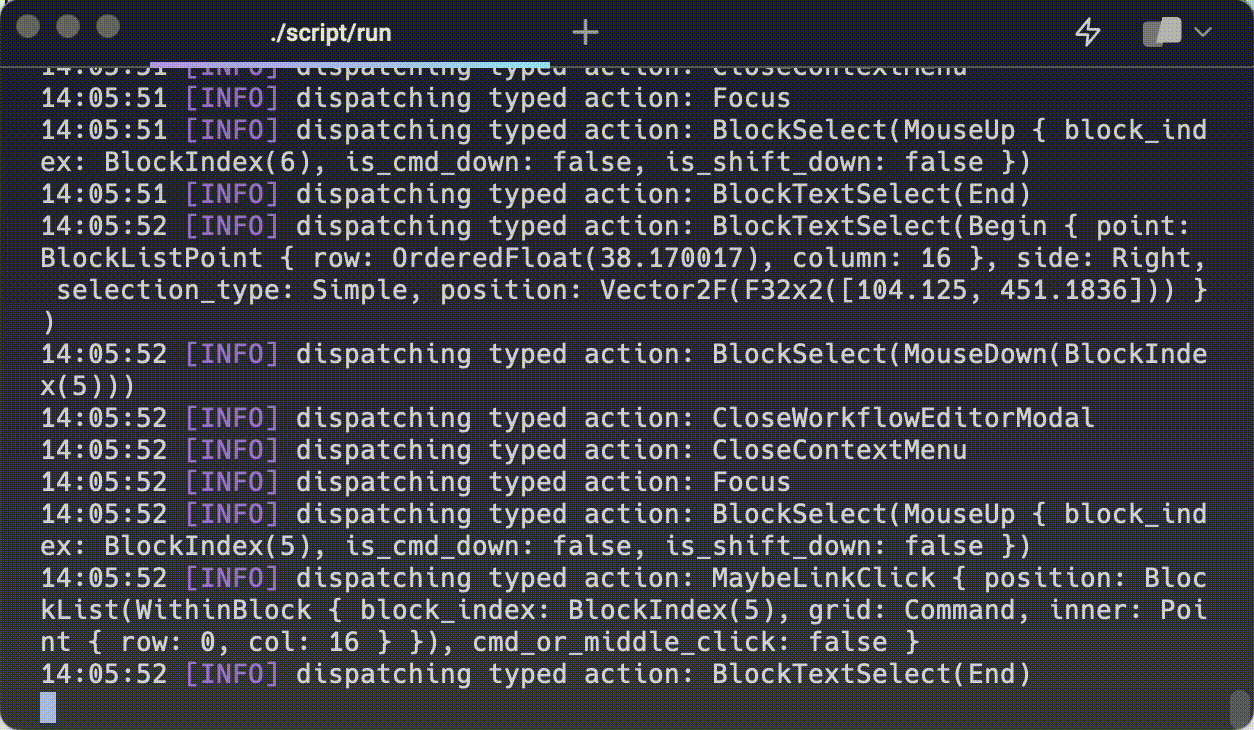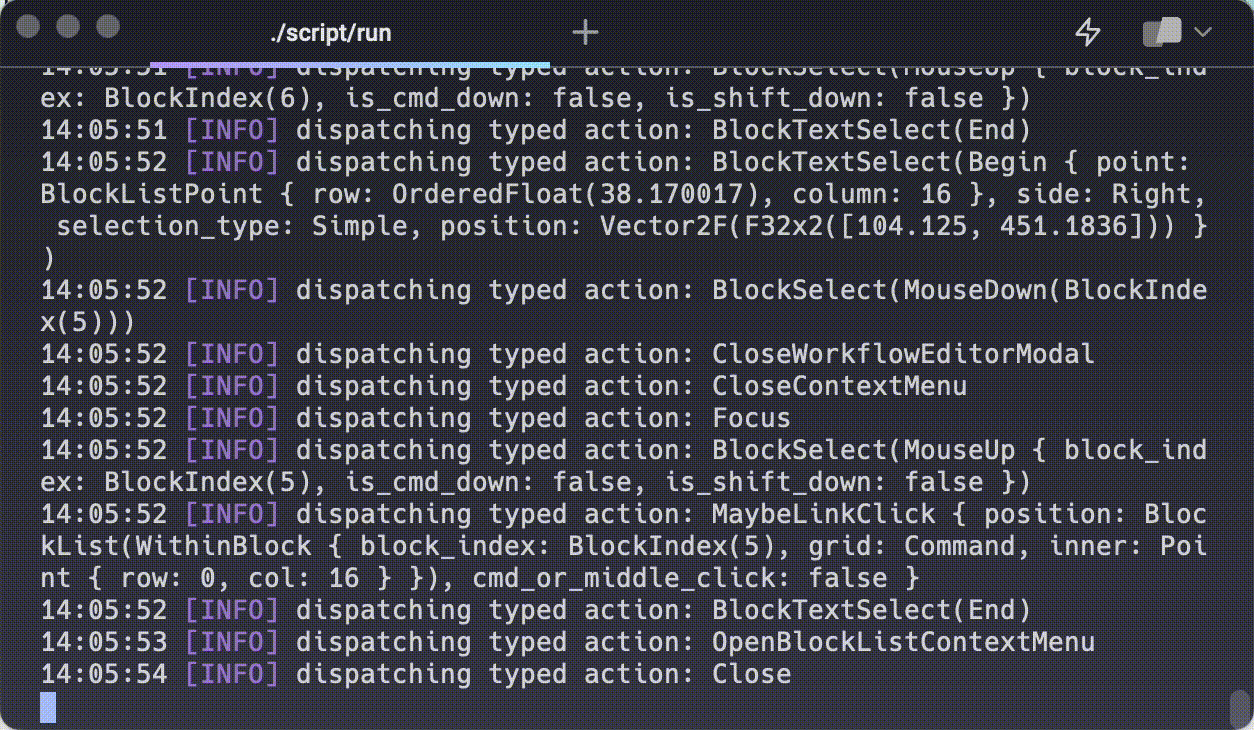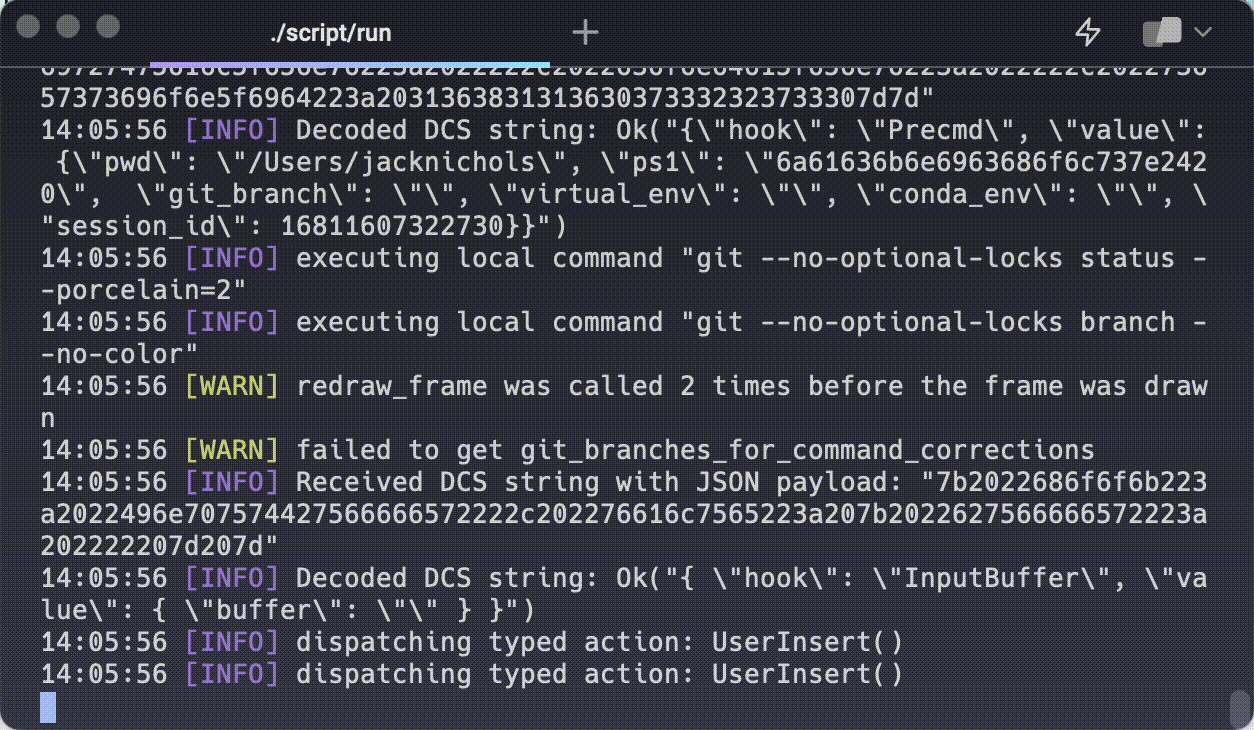
Here, the terminal reads content from the shell (via the receiving end of a pipe known as the PTY, short for pseudo-TTY) and writes it to a grid. This is a fundamental operation for the terminal: how efficiently can we read streamed input from an open file descriptor and write it character-by-character to the specified grid location?

Specifically, the problem becomes interesting in the common case where the shell issues a newline – this is the shell warning the terminal that the command requires more than the current size of the grid, implying the vertical grid dimension needs to be expanded by one row. From the terminal’s perspective, let’s consider this request under the worst-case grid configuration: the underlying vector is already at capacity and the grid is rotated (again, index on screen != index in vector).

Capacity:if the vector has no more free memory, then we cannot avoid a vector resize cost. Vectors are heap-allocated data types, and resizing requires (1) finding a heap chunk that’s big enough for the new capacity and (2) copying the old contents into the new memory space.⁷
Rotation: if the grid is currently rotated, then we must “re-zero” the vector before increasing its size. This implies costly memory management: we reverse the rotation until the conceptual “top row” is back to vector index 0. Only once the vector is unrotated can we tag new rows onto the end.

Here, we cannot extend the vector until the existing contents are unrotated. Otherwise, we’d conceptually be tagging on new rows to somewhere that’s not the end of the logical grid - that would be a mess! This “re-zero” is a costly copying operation.

Because the penalty under the worst-case grid configuration is very high, Warp does its best to make this circumstance as infrequent as possible. As an example, we only allocate new rows in chunks of 1000, opting to make the resize slightly more heavyweight with the benefit of amortizing the cost to every 1000 newlines.

Resizing a grid

A final, essential piece to this weaving narrative about grid optimizations and their externalities is the process of resizing a grid. Importantly, grids in Warp are always stored at the dimensions of the pane in which they render, which are not necessarily equivalent to the dimensions at which we received them from the shell. Said differently, we always rewrite the grid so any horizontal limit is imposed at the time of resizing and not at the time of rendering. This makes more sense with a visual:

If the shell originally outputs a grid that is 10 rows by 10 columns and the user proceeds to resize the screen (or split a pane) that makes the grid 5 columns, then internally the vector is re-written to account for this new horizontal constraint: the grid becomes 20 rows by 5 columns both on screen and in storage. Today, every resize in Warp requires re-writing every grid currently displayed on the screen from the top down, row by row.

We permit this considerable performance penalty – for now – because, although resizing is an essential operation, it’s hard designing optimizations that won’t slow down everything else: doing index conversions, scrolling, adding a new line to the grid, etc. From a holistic standpoint about overall performance priorities in the app, it’s also not clear that resizing should take precedence over any of those things.

Conclusion

All told, an intelligent, intentional design of the terminal grid should recognize that oftentimes the most important operations are in competition with one another. Every block in Warp is a careful calculus about where to excel and how to minimize the resulting cost: that the rotated vector streamlines scrolling but costs us the amortized “re-zero” every 1000 lines, that allocating new rows in chunks means we’re willing to risk some bloat for fewer memory allocations, that storing the grid in its renderable dimensions is optimal but leaves us vulnerable at resize, to name but a few.

If you have opinions on what our performance priorities should be – or any insights about the trade-offs discussed here – we’d love to hear from you! Better yet, if you find this type of problem interesting, come work with us!

¹^{The short answer: probably yes. All grids in Warp are initialized to be roughly the size of the visible screen. On average, this is usually about 30 – 50 rows, although there’s no reason it couldn’t be much smaller or much bigger. When the grid is filled up, it is indeed an extra 1000 rows that are pre-allocated under the assumption that if a command asks for one extra row it will probably ask for many more. After the command is finished, the grid is truncated down and any unused rows at the end of the grid are freed up.}

²^{We used Alacritty’s model code as the source of our initial grid implementation. We’ve made some tweaks to better fit our use case, but many of the design decisions mentioned here came from their original implementation.}

³^{This is an active area of focus in Warp. Originally, we stored the rows in reversed order but there’s a project underway to just store the rows sequentially.}

⁴^{Question: this seems to be using bottom_row just to compute the “top row” (where screen index = 0) and it does that for every conversion. Why not just store the “top row” index instead of the bottom? Answer: It’s a really good question. The reality is that converting between “bottom row” and “top row” is some fixed cost of a couple arithmetic operations and, while it’s probably meaningless in most cases, it’s ever-so-slightly preferably to pay this penalty at the time of rendering the grid than at the time of writing the contents of the grid, where it’s a neat optimization to quickly know where the next line of output goes.}

⁵^{There’s a small distinction here because scrolling in the blocklist actually generally doesn’t modify grids at all. We have our own viewport system that enables scrolling independent of grids. vim, emacs, git log, git diff are listed here as examples of commands that do use grid scrolling.}

⁶^{There are open-source terminal performance benchmarks that track exactly this: vtebenchand termbench.}

⁷^{https://doc.rust-lang.org/std/vec/struct.Vec.html}

⁸^{This is an active topic of conversation at Warp. One idea for how to fix this performance problem is to introduce asynchronicity to the resize process.}

The data structure behind terminals

Getting technical²

Scrolling the grid

Extending the grid

Resizing a grid

Conclusion

Related

Download Warp
to get started

The data structure behind terminals

Getting technical2

Scrolling the grid

Extending the grid

Resizing a grid

Conclusion

Related

Download Warp to get started

Getting technical²

Download Warp
to get started